全排列问题

排列 (Permutation) 是将相异对象或符号根据确定的顺序重排。每个顺序都称作一个排列。

从n个不同元素中任取m（m≤n）个元素，按照一定的顺序排列起来，叫做从n个不同元素中取出m个元素的一个排列。当m=n时所有的排列情况叫全排列。

全排列问题常出现在串（string） 相关的问题中。

例题：

1. 递归DFS+剪枝解法

最佳子结构设计

长度为n的串的全排列问题可以分为以下的子问题结构：

a = 长度为n-1的串有多少种排列
b = 插入的元素有多少种可能

最后的结果显然为 a+b

那么如何得到长度为n-1的串的排列数呢？

我们先固定一种串的排列方式，通过字符交换的方式，依次固定第i个字符，直到固定第n个字符时即为一种排列方式。

遍历途中对于固定的第i个字符，剩下的 (n-i) 个字符，则是需要递归处理的子问题。

但是，这种方法对于含有重复元素的集合会产生重复串（不适用重复元素）。

按照上述的最佳子结构关系，以串 1234 为例构建递归如下图所示，边界情况为子串长度=1：

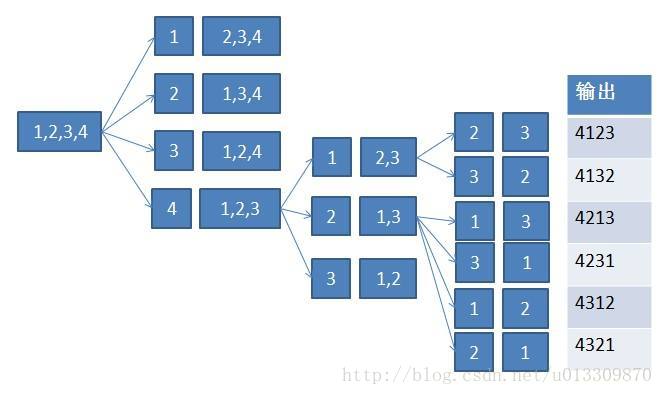
剪枝

我们不妨思考一下，为什么会产生重复串呢？

因为在交换的时候，对于固定位chs[i]，后面若有两个重复字符，就会与之交换两次，虽然当时是不重复的，但在后续的交换中就会产生重复串。

如串abccd，在固定a时会与c交换两次，生成两个串cbacd和cbcad。虽然此时这是不重复的，但我们在DFS树中更深入一点，在cbacd这个分支里，固定位到a时，也会因交换产生cbcad这个串，这样就产生了重复。

因此，如果我们在分支的上游就排除了相同字符交换产生的分支（剪枝），不仅可以避免重复，还可以避免大量重复计算。

具体的实现，我们可以通过一个HashSet（其内的元素不允许重复，具有集合的特征，详见容器篇）来记录当前交换过程内所有已经交换过的字符来实现剪枝。

代码

C#题解如下：

public class Permutation
  {
    static public List<string> Result = new List<string>();
    static T[] Swap<T>(T[] source, int i1, int i2)
    {
      var t = source[i2];
      source[i2] = source[i1];
      source[i1] = t;
      return source;
    }
    static public string[] Recursively(string str)
    {
      var candidate = str.ToCharArray();
      Recursively(candidate, 0);
      var res = Result.ToArray();
      Result.Clear();
      return res;
    }
    static void Recursively(char[] charSet, int start)
    {
      if (start == charSet.Length - 1)
      {
        var str = new String(charSet);
        Console.WriteLine(str);
        Result.Add(str);
      }
      var set = new HashSet<char>();
      for (int i = start; i < charSet.Length; i++)
      {
        if (i == start || charSet[i] != charSet[start])
        {
          if (set.Contains(charSet[i])) continue;
          set.Add(charSet[i]);
          Swap(charSet, start, i);
          Recursively(charSet, start + 1);
          Swap(charSet, start, i); // 还原变化
        }
      }
    }
  }

字典序排列

下一个排列数

一个（数字）序列的字典序是这些数字（如 {1, 2, 3, 4}）组成的串大小（如1234）按升序排列的顺序，下一个排列就是对应串 (如12354) 在字典序中的下一个序列 (如12435)。

为了得到下一个更大的最小序列数（比当前大，但增加的幅度尽量小），我们构造如下算法要求：

为了比当前大，我们需要将后面的大数（低位大数）与前面的小数交换（高位小数）
为了增大的尽量小，我们要满足以下要求：
- 交换的位越靠右越好（位数越低增加得越少）
- 将右边最小的大数用于交换
- 交换后还要保证右边的序列是最小的（逆序排列）

最后，我们构造算法如下：

从后向前 查找第一个 相邻升序 的元素对 (i,j)，满足 A[i] < A[j]。此时 [j,end) 必然是降序
在 [j,end) 从后向前 查找第一个满足 A[i] < A[k] 的 k。A[i]、A[k] 分别就是上文所说的「小数」、「大数」
将 A[i] 与 A[k] 交换
可以断定这时 [j,end) 必然是降序，逆置 [j,end)，使其升序
如果在步骤 1 找不到符合的相邻元素对，说明当前 [begin,end) 为一个降序顺序，则直接跳到步骤 4【最大序列跳回最小序列】

C# 实现为：

public void NextPermutation(int[] nums)
{
  int i;
  for (i = nums.Length - 1; i > 0; i--)
  {
    if (nums[i - 1] < nums[i]) // 找到第一个升序对
    {
      for (int j = nums.Length - 1; j >= i; j--)
      {
        if (nums[j] > nums[i - 1]) // 找到最小交换位置
        {
          Swap(nums, j, i - 1);
          break;
        }
      }
      break;
    }
  }
  int left = i, right = nums.Length - 1;
  while (left < right) // 逆序排列
  {
    Swap(nums, left, right);
    left++;
    right--;
  }
}

解决字符串排列问题

直接把串化为字符数组，然后对这个数组排序，得到初始字典序，反复求下一个排列直到最大排序。

先输出初始序列：1234
从右向左找到第一个非递增的数（比前一个数小的数）：3
交换这个数与前一个数，并一路移动到右边序列末尾，输出序列：1243 （31. 下一个全排列数）
循环直到找不到更大的排列数

这个方法的优势在于：没有递归栈，省去了反复函数调用的开销。

ChlorineC's Blog